Rectangular parallelepiped. Parallelepiped and cube

CHAPTER THREE

POLYhedra

1. PARALLELEPIPED AND PYRAMID

Properties of faces and diagonals of a parallelepiped

72. Theorem. In a parallelepiped:

1)opposite sides are equal and parallel;

2) all four diagonals intersect at one point and bisect there.

1) The faces (Fig. 80) BB 1 C 1 C and AA 1 D 1 D are parallel, because two intersecting straight lines BB 1 and B 1 C 1 of one face are parallel to two intersecting straight lines AA 1 and A 1 D 1 of the other (§ 15 ); these faces are equal, since B 1 C 1 = A 1 D 1, B 1 B = A 1 A (like opposite sides of parallelograms) and / BB 1 C 1 = / AA 1 D 1 .

2) Take (Fig. 81) some two diagonals, for example AC 1 and ВD 1, and draw auxiliary lines AD 1 and ВС 1.

Since the edges AB and D 1 C 1 are respectively equal and parallel to the edge DC, they are equal and parallel to each other; As a result, the figure AD 1 C 1 B is a parallelogram in which the straight lines C 1 A and BD 1 are diagonals, and in a parallelogram the diagonals are divided in half at the point of intersection.

Let us now take one of these diagonals, for example AC 1, with a third diagonal, let us say, with B 1 D. In exactly the same way we can prove that they are divided in half at the point of intersection. Consequently, diagonals B 1 D and AC 1 and diagonals AC 1 and BD 1 (which we took earlier) intersect at the same point, precisely in the middle of the diagonal
AC 1. Finally, taking the same diagonal AC 1 with the fourth diagonal A 1 C, we also prove that they are bisected. This means that the point of intersection of this pair of diagonals lies in the middle of the diagonal AC 1. Thus, all four diagonals of the parallelepiped intersect at the same point and are bisected by this point.

73. Theorem. In a rectangular parallelepiped, the square of any diagonal (AS 1, drawing 82) equal to the sum of the squares of its three dimensions .

Drawing the diagonal of the base AC, we obtain triangles AC 1 C and ACB. Both of them are rectangular: the first because the parallelepiped is straight and, therefore, edge CC 1 is perpendicular to the base; the second because the parallelepiped is rectangular and, therefore, a rectangle lies at its base. From these triangles we find:

AC 1 2 = AC 2 + CC 1 2 and AC 2 = AB 2 + BC 2

Hence,

AC 1 2 = AB 2 + BC 2 + CC 1 2 = AB 2 + AD 2 + AA 1 2.

Consequence.In a rectangular parallelepiped, all diagonals are equal.

Theorem. In any parallelepiped, opposite faces are equal and parallel.

Thus, the faces (Fig.) BB 1 C 1 C and AA 1 D 1 D are parallel, because two intersecting lines BB 1 and B 1 C 1 of one face are parallel to two intersecting lines AA 1 and A 1 D 1 of the other. These faces are equal, since B 1 C 1 =A 1 D 1, B 1 B=A 1 A (as opposite sides of parallelograms) and ∠BB 1 C 1 = ∠AA 1 D 1.

Theorem. In any parallelepiped, all four diagonals intersect at one point and are bisected at it.

Let's take (Fig.) some two diagonals in the parallelepiped, for example, AC 1 and DB 1, and draw straight lines AB 1 and DC 1.

Since the edges AD and B 1 C 1 are respectively equal and parallel to the edge BC, then they are equal and parallel to each other.

As a result, the figure ADC 1 B 1 is a parallelogram in which C 1 A and DB 1 are diagonals, and in a parallelogram the diagonals intersect in half.

This proof can be repeated for every two diagonals.

Therefore, diagonal AC 1 intersects BD 1 in half, diagonal BD 1 intersects A 1 C in half.

Thus, all diagonals intersect in half and, therefore, at one point.

Theorem. In a rectangular parallelepiped, the square of any diagonal is equal to the sum of the squares of its three dimensions.

Let (Fig.) AC 1 be some diagonal of a rectangular parallelepiped.

Drawing AC, we get two triangles: AC 1 C and ACB. Both of them are rectangular:

the first because the parallelepiped is straight, and therefore edge CC 1 is perpendicular to the base,

the second because the parallelepiped is rectangular, which means that there is a rectangle at its base.

From these triangles we find:

AC 2 1 = AC 2 + CC 2 1 and AC 2 = AB 2 + BC 2

Therefore, AC 2 1 = AB 2 + BC 2 + CC 2 1 = AB 2 + AD 2 + AA 2 1

Consequence. In a rectangular parallelepiped all diagonals are equal.

Maintaining your privacy is important to us. For this reason, we have developed a Privacy Policy that describes how we use and store your information. Please review our privacy practices and let us know if you have any questions.

Collection and use of personal information

Personal information refers to data that can be used to identify or contact a specific person.

You may be asked to provide your personal information at any time when you contact us.

Below are some examples of the types of personal information we may collect and how we may use such information.

What personal information do we collect:

• When you submit an application on the site, we may collect various information, including your name, phone number, email address, etc.

How we use your personal information:

• The personal information we collect allows us to contact you with unique offers, promotions and other events and upcoming events.
• From time to time, we may use your personal information to send important notices and communications.
• We may also use personal information for internal purposes, such as conducting audits, data analysis and various research in order to improve the services we provide and provide you with recommendations regarding our services.
• If you participate in a prize draw, contest or similar promotion, we may use the information you provide to administer such programs.

Disclosure of information to third parties

We do not disclose the information received from you to third parties.

Exceptions:

• If necessary - in accordance with the law, judicial procedure, in legal proceedings, and/or on the basis of public requests or requests from government authorities in the territory of the Russian Federation - to disclose your personal information. We may also disclose information about you if we determine that such disclosure is necessary or appropriate for security, law enforcement, or other public importance purposes.
• In the event of a reorganization, merger, or sale, we may transfer the personal information we collect to the applicable successor third party.

Protection of personal information

We take precautions - including administrative, technical and physical - to protect your personal information from loss, theft, and misuse, as well as unauthorized access, disclosure, alteration and destruction.

Respecting your privacy at the company level

To ensure that your personal information is secure, we communicate privacy and security standards to our employees and strictly enforce privacy practices.

In this lesson, everyone will be able to study the topic “Rectangular parallelepiped”. At the beginning of the lesson, we will repeat what arbitrary and straight parallelepipeds are, remember the properties of their opposite faces and diagonals of the parallelepiped. Then we'll look at what a cuboid is and discuss its basic properties.

Topic: Perpendicularity of lines and planes

Lesson: Cuboid

A surface composed of two equal parallelograms ABCD and A 1 B 1 C 1 D 1 and four parallelograms ABV 1 A 1, BCC 1 B 1, CDD 1 C 1, DAA 1 D 1 is called parallelepiped(Fig. 1).

Rice. 1 Parallelepiped

That is: we have two equal parallelograms ABCD and A 1 B 1 C 1 D 1 (bases), they lie in parallel planes so that the side edges AA 1, BB 1, DD 1, CC 1 are parallel. Thus, a surface composed of parallelograms is called parallelepiped.

Thus, the surface of a parallelepiped is the sum of all the parallelograms that make up the parallelepiped.

1. The opposite faces of a parallelepiped are parallel and equal.

(the shapes are equal, that is, they can be combined by overlapping)

For example:

ABCD = A 1 B 1 C 1 D 1 (equal parallelograms by definition),

AA 1 B 1 B = DD 1 C 1 C (since AA 1 B 1 B and DD 1 C 1 C are opposite faces of the parallelepiped),

AA 1 D 1 D = BB 1 C 1 C (since AA 1 D 1 D and BB 1 C 1 C are opposite faces of the parallelepiped).

2. The diagonals of a parallelepiped intersect at one point and are bisected by this point.

The diagonals of the parallelepiped AC 1, B 1 D, A 1 C, D 1 B intersect at one point O, and each diagonal is divided in half by this point (Fig. 2).

Rice. 2 The diagonals of a parallelepiped intersect and are divided in half by the intersection point.

3. There are three quadruples of equal and parallel edges of a parallelepiped: 1 - AB, A 1 B 1, D 1 C 1, DC, 2 - AD, A 1 D 1, B 1 C 1, BC, 3 - AA 1, BB 1, CC 1, DD 1.

Definition. A parallelepiped is called straight if its lateral edges are perpendicular to the bases.

Let the side edge AA 1 be perpendicular to the base (Fig. 3). This means that straight line AA 1 is perpendicular to straight lines AD and AB, which lie in the plane of the base. This means that the side faces contain rectangles. And the bases contain arbitrary parallelograms. Let us denote ∠BAD = φ, the angle φ can be any.

Rice. 3 Right parallelepiped

So, a right parallelepiped is a parallelepiped in which the side edges are perpendicular to the bases of the parallelepiped.

Definition. The parallelepiped is called rectangular, if its lateral edges are perpendicular to the base. The bases are rectangles.

The parallelepiped ABCDA 1 B 1 C 1 D 1 is rectangular (Fig. 4), if:

1. AA 1 ⊥ ABCD (lateral edge perpendicular to the plane of the base, that is, a straight parallelepiped).

2. ∠BAD = 90°, i.e. the base is a rectangle.

Rice. 4 Rectangular parallelepiped

A rectangular parallelepiped has all the properties of an arbitrary parallelepiped. But there are additional properties that are derived from the definition of a cuboid.

So, cuboid is a parallelepiped whose side edges are perpendicular to the base. The base of a cuboid is a rectangle.

1. In a rectangular parallelepiped, all six faces are rectangles.

ABCD and A 1 B 1 C 1 D 1 are rectangles by definition.

2. Lateral ribs are perpendicular to the base. This means that all the lateral faces of a rectangular parallelepiped are rectangles.

3. All dihedral angles of a rectangular parallelepiped are right.

Let us consider, for example, the dihedral angle of a rectangular parallelepiped with edge AB, i.e., the dihedral angle between planes ABC 1 and ABC.

AB is an edge, point A 1 lies in one plane - in the plane ABB 1, and point D in the other - in the plane A 1 B 1 C 1 D 1. Then the dihedral angle under consideration can also be denoted as follows: ∠A 1 ABD.

Let's take point A on edge AB. AA 1 is perpendicular to edge AB in the plane АВВ-1, AD is perpendicular to edge AB in the plane ABC. This means that ∠A 1 AD is the linear angle of a given dihedral angle. ∠A 1 AD = 90°, which means that the dihedral angle at edge AB is 90°.

∠(ABB 1, ABC) = ∠(AB) = ∠A 1 ABD= ∠A 1 AD = 90°.

Similarly, it is proved that any dihedral angles of a rectangular parallelepiped are right.

The square of the diagonal of a rectangular parallelepiped is equal to the sum of the squares of its three dimensions.

Note. The lengths of the three edges emanating from one vertex of a cuboid are the measurements of the cuboid. They are sometimes called length, width, height.

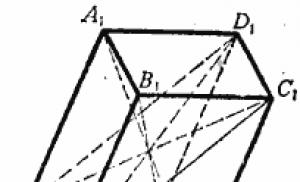
Given: ABCDA 1 B 1 C 1 D 1 - rectangular parallelepiped (Fig. 5).

Prove: .

Rice. 5 Rectangular parallelepiped

Proof:

Straight line CC 1 is perpendicular to plane ABC, and therefore to straight line AC. This means that the triangle CC 1 A is right-angled. According to the Pythagorean theorem:

Consider the right triangle ABC. According to the Pythagorean theorem:

But BC and AD are opposite sides of the rectangle. So BC = AD. Then:

Because , A , That. Since CC 1 = AA 1, this is what needed to be proven.

The diagonals of a rectangular parallelepiped are equal.

Let us denote the dimensions of the parallelepiped ABC as a, b, c (see Fig. 6), then AC 1 = CA 1 = B 1 D = DB 1 =

A cuboid is a type of polyhedron consisting of 6 faces, each of which is a rectangle. In turn, a diagonal is a segment that connects the opposite vertices of a parallelogram. Its length can be determined in two ways.

You will need

• Knowing the lengths of all sides of a parallelogram.

Instructions

1. Method 1. Given a rectangular parallelepiped with sides a, b, c and diagonal d. According to one of the properties of a parallelogram, the square of the diagonal is equal to the sum of the squares of its 3 sides. It follows that the length of the diagonal itself can be calculated by extracting the square from a given sum (Fig. 1).

2. Method 2. It is possible that the rectangular parallelepiped is a cube. A cube is a rectangular parallelepiped in which every face is represented by a square. Consequently, all its sides are equal. Then the formula for calculating the length of its diagonal will be expressed as follows: d = a*?3

A parallelepiped is a special case of a prism, in which all six faces are parallelograms or rectangles. A parallelepiped with rectangular faces is also called rectangular. A parallelepiped has four intersecting diagonals. If three edges a, b, c are given, you can find all the diagonals of a rectangular parallelepiped by performing additional constructions.

Instructions

1. Draw a rectangular parallelepiped. Write down the known data: three edges a, b, c. First construct one diagonal m. To determine it, we use the quality of a rectangular parallelepiped, according to which all its angles are right.

2. Construct the diagonal n of one of the faces of the parallelepiped. Carry out the construction so that the famous edge, the desired diagonal of the parallelepiped and the diagonal of the face together form a right triangle a, n, m.

3. Find the constructed diagonal of the face. It is the hypotenuse of another right triangle b, c, n. According to the Pythagorean theorem, n² = c² + b². Calculate this expression and take the square root of the resulting value - this will be the diagonal of face n.

4. Find the diagonal of the parallelepiped m. To do this, in the right triangle a, n, m, find an unfamiliar hypotenuse: m² = n² + a². Substitute the known values, then calculate the square root. The resulting result will be the first diagonal of the parallelepiped m.

5. Similarly, draw all the other three diagonals of the parallelepiped in steps. Also, for all of them, perform additional construction of diagonals of adjacent faces. By looking at the right triangles formed and applying the Pythagorean theorem, discover the values ​​of the remaining diagonals of the cuboid.

Video on the topic

Many real objects have a parallelepiped shape. Examples are the room and the pool. Parts with this shape are not uncommon in industry. For this reason, the task of finding the volume of a given figure often arises.

Instructions

1. A parallelepiped is a prism whose base is a parallelogram. A parallelepiped has faces - all the planes that form this figure. Each of them has six faces, and all of them are parallelograms. Its opposite sides are equal and parallel to each other. In addition, it has diagonals that intersect at one point and bisect at it.

2. There are 2 types of parallelepiped. For the first, all faces are parallelograms, and for the second, they are rectangles. The final one is called a rectangular parallelepiped. All its faces are rectangular, and the side faces are perpendicular to the base. If a rectangular parallelepiped has faces whose bases are squares, then it is called a cube. In this case, its faces and edges are equal. An edge is a side of any polyhedron, which includes a parallelepiped.

3. In order to find the volume of a parallelepiped, you need to know the area of ​​its base and height. The volume is found based on which particular parallelepiped appears in the conditions of the problem. An ordinary parallelepiped has a parallelogram at its base, while a rectangular one has a rectangle or a square, which invariably has right angles. If there is a parallelogram at the base of a parallelepiped, then its volume is found as follows: V = S * H, where S is the area of ​​the base, H is the height of the parallelepiped. The height of a parallelepiped is usually its lateral edge. At the base of a parallelepiped there can also be a parallelogram that is not a rectangle. From the course of planimetry it is known that the area of ​​a parallelogram is equal to: S=a*h, where h is the height of the parallelogram, a is the length of the base, i.e. :V=a*hp*H

4. If the 2nd case occurs, when the base of the parallelepiped is a rectangle, then the volume is calculated using the same formula, but the area of ​​the base is found in a slightly different way: V=S*H,S=a*b, where a and b are the sides, respectively rectangle and parallelepiped edge.V=a*b*H

5. To find the volume of a cube, one should be guided by primitive logical methods. Since all the faces and edges of the cube are equal, and at the base of the cube there is a square, guided by the formulas indicated above, we can derive the following formula: V = a^3

A closed geometric figure formed by two pairs of parallel segments of identical length lying opposite each other is called a parallelogram. A parallelogram, all angles of which are equal to 90°, is also called a rectangle. In this figure, you can draw two segments of identical length connecting opposite vertices - diagonals. The length of these diagonals is calculated by several methods.

Instructions

1. If the lengths of 2 adjacent sides are known rectangle(A and B), then the length of the diagonal (C) is very simple to determine. Proceed from the fact that diagonal lies opposite the right angle in the triangle formed by it and these two sides. This allows us to apply the Pythagorean theorem in calculations and calculate the length of the diagonal by finding the square root of the sum of the squared lengths of the leading sides: C = v (A? + B?).

2. If the length of only one side is known rectangle(A), as well as the size of the angle (?), the one that forms with it diagonal, then to calculate the length of this diagonal (C) you will have to use one of the direct trigonometric functions - cosine. Divide the length of the leading side by the cosine of the famous angle - this will be the desired length of the diagonal: C=A/cos(?).

3. If a rectangle is given by the coordinates of its vertices, then the task of calculating the length of its diagonal will be reduced to finding the distance between two points in this coordinate system. Apply the Pythagorean theorem to the triangle that forms the projection of the diagonal on each of the coordinate axes. It is possible that a rectangle in two-dimensional coordinates is formed by the vertices A(X?;Y?), B(X?;Y?), C(X?;Y?) and D(X?;Y?). Then you need to calculate the distance between points A and C. The length of the projection of this segment onto the X axis will be equal to the modulus of the coordinate difference |X?-X?|, and the projection onto the Y axis – |Y?-Y?|. The angle between the axes is 90°, from which it follows that these two projections are legs, and the length of the diagonal (hypotenuse) is equal to the square root of the sum of the squares of their lengths: AC=v((X?-X?)?+(Y?- Y?)?).

4. To find the diagonal rectangle in a three-dimensional coordinate system, proceed in the same way as in the previous step, only adding to the formula the length of the projection onto the third coordinate axis: AC=v((X?-X?)?+(Y?-Y?)?+(Z?- Z?)?).

Video on the topic

A mathematical joke remains in the memory of many: Pythagorean pants are equal in all directions. Use it to calculate diagonal rectangle .

You will need

• A sheet of paper, a ruler, a pencil, a calculator with a function for calculating roots.

Instructions

1. A rectangle is a quadrilateral whose angles are all right. Diagonal rectangle- a straight line segment connecting its two opposite vertices.

2. On a piece of paper supported by a ruler and pencil, draw an arbitrary rectangle ABCD. It’s cooler to do this on a squared notebook sheet - it will be easier to draw right angles. Connect the vertices with a segment rectangle A and C. The resulting segment AC is diagonal Yu rectangle ABCD.

3. Note, diagonal AC divides rectangle ABCD into triangles ABC and ACD. The resulting triangles ABC and ACD are right triangles, because angles ABC and ADC are equal to 90 degrees (by definition rectangle). Remember the Pythagorean theorem - the square of the hypotenuse is equal to the sum of the squares of the legs.

4. The hypotenuse is the side of the triangle opposite the right angle. Legs are the sides of a triangle adjacent to a right angle. In relation to triangles ABC and ACD: AB and BC, AD and DC are legs, AC is the universal hypotenuse for both triangles (desired diagonal). Consequently, AC squared = square AB + square BC or AC squared = square AD + square DC. Substitute the side lengths rectangle into the above formula and calculate the length of the hypotenuse (diagonal rectangle).

5. Let's say the sides rectangle ABCD are equal to the following values: AB = 5 cm and BC = 7 cm. The square of the diagonal AC of a given rectangle calculated using the Pythagorean theorem: AC squared = square AB + square BC = 52+72 = 25 + 49 = 74 sq.cm. Using a calculator, calculate the square root of 74. You should get 8.6 cm (rounded value). Please note that according to one of the properties rectangle, its diagonals are equal. So the length of the 2nd diagonal BD rectangle ABCD is equal to the length of diagonal AC. For the example above, this value is 8.6 cm.

Video on the topic

Tip 6: How to find the diagonal of a parallelogram given the sides

A parallelogram is a quadrilateral whose opposite sides are parallel. The straight lines connecting its opposite angles are called diagonals. Their length depends not only on the lengths of the sides of the figure, but also on the values ​​of the angles at the vertices of this polygon; therefore, without knowing the truth of one of the angles, calculating the lengths of the diagonals is allowed only in exceptional cases. These are special cases of parallelograms - square and rectangle.

Instructions

1. If the lengths of all sides of a parallelogram are identical (a), then this figure can also be called a square. The values ​​of all its angles are equal to 90°, and the lengths of the diagonals (L) are identical and can be calculated using the Pythagorean theorem for a right triangle. Multiply the length of the side of the square by the root of two - the result will be the length of each of its diagonals: L=a*?2.

2. If it is known about a parallelogram that it is a rectangle with the length (a) and width (b) indicated in the conditions, then in this case the lengths of the diagonals (L) will be equal. And here, too, use the Pythagorean theorem for a triangle in which the hypotenuse is the diagonal, and the legs are two adjacent sides of the quadrilateral. Calculate the desired value by taking the root of the sum of the squared width and height of the rectangle: L=?(a?+b?).

3. For all other cases, the skill of the side lengths alone is sufficient only to determine a value that includes the lengths of both diagonals at once - the sum of their squares, by definition, is equal to twice the sum of the squares of the side lengths. If, in addition to the lengths of the two adjacent sides of the parallelogram (a and b), the angle between them (?) is also known, then this will allow us to calculate the lengths of any segment connecting the opposite corners of the figure. Find the length of the diagonal (L?), lying opposite the given angle, using the cosine theorem - add the squares of the lengths of adjacent sides, subtract from the total the product of the same lengths by the cosine of the angle between them, and from the resulting value take the square root: L? = ?(a?+b?-2*a*b*cos(?)). To find the length of another diagonal (L?), you can use the property of a parallelogram given at the beginning of this step - double the sum of the squares of the lengths of 2 sides, subtract the square of the calculated diagonal from the total, and take the root from the resulting value. In general, this formula can be written as follows: L? = ?(a?+b?- L??) = ?(a?+b?-(a?+b?-2*a*b*cos(?))) = ?(a?+b?- a?-b?+2*a*b*cos(?)) = ?(2*a*b*cos(?)).