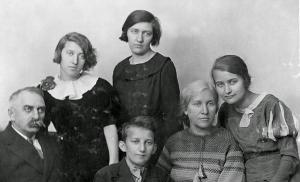Прямоугольный параллелепипед. Параллелепипед и куб

ГЛАВА ТРЕТЬЯ

МНОГОГРАННИКИ

1. ПАРАЛЛЕЛЕПИПЕД И ПИРАМИДА

Свойства граней и диагоналей параллелепипеда

72. Теорема. В параллелепипеде:

1) противоположные грани равны и параллельны;

2) все четыре диагонали пересекаются в одной точке и делятся в ней пополам.

1) Грани (черт. 80) ВВ 1 С 1 С и AA 1 D 1 D параллельны, потому что две пересекающиеся прямые ВВ 1 и В 1 С 1 одной грани параллельны двум пересекающимся прямым АА 1 и A 1 D 1 другой (§ 15); эти грани и равны, так как В 1 С 1 = A 1 D 1 , В 1 В= А 1 А (как противоположные стороны параллелограммов) и / ВВ 1 С 1 = / АA 1 D 1 .

2) Возьмём (черт. 81) какие-нибудь две диагонали, например АС 1 и ВD 1 , и проведём вспомогательные прямые АD 1 и ВС 1 .

Так как рёбра АВ и D 1 С 1 соответственно равны и параллельны ребру DС, то они равны и параллельны между собой; вследствие этого фигура АD 1 С 1 В есть параллелограмм, в котором прямые С 1 А и ВD 1 -диагонали, а в параллелограмме диагонали делятся в точке пересечения пополам.

Возьмём теперь одну из этих диагоналей, например АС 1 , с третьей диагональю, положим, с В 1 D. Совершенно так же мы можем доказать, что они делятся в точке пересечения пополам. Следовательно, диагонали B 1 D и АС 1 и диагонали АС 1 и BD 1 (которые мы раньше брали) пересекаются в одной и той же точке, именно в середине диагонали
АС 1 . Наконец, взяв эту же диагональ АС 1 с четвёртой диагональю А 1 С, мы также докажем, что они делятся пополам. Значит, точка пересечения и этой пары диагоналей лежит в середине диагонали АС 1 . Таким образом, все четыре диагонали параллелепипеда пересекаются в одной и той же точке и делятся этой точкой пополам.

73. Теорема. В прямоугольном параллелепипеде квадрат любой диагонали (АС 1 , черт. 82) равен сумме квадратов трёх его измерений .

Проведя диагональ основания АС, получим треугольники АС 1 С и АСВ. Оба они прямоугольные: первый потому, что параллелепипед прямой и, следовательно, ребро СС 1 перпендикулярно к основанию; второй потому, что параллелепипед прямоугольный и, значит, в основании его лежит прямоугольник. Из этих треугольников находим:

АС 1 2 = АС 2 + СС 1 2 и АС 2 = АВ 2 + ВС 2

Следовательно,

AC 1 2 = АВ 2 + ВС 2 + СС 1 2 = АВ 2 + AD 2 + АА 1 2 .

Следствие. В прямоугольном параллелепипеде все диагонали равны.

Теорема. Во всяком параллелепипеде противоположные грани равны и параллельны.

Так, грани (рис.) BB 1 С 1 С и AA 1 D 1 D параллельны, потому, что две пересекающиеся прямые BB 1 и B 1 С 1 одной грани параллельны двум пересекающимся прямым AA 1 и A 1 D 1 другой. Эти грани и равны, так как B 1 С 1 =A 1 D 1 , B 1 B=A 1 A (как противоположные стороны параллелограммов) и ∠BB 1 С 1 = ∠AA 1 D 1 .

Теорема. Во всяком параллелепипеде все четыре диагонали пересекаются в одной точке и делятся в ней пополам.

Возьмем (рис.) в параллелепипеде какие-нибудь две диагонали, например, AС 1 и DB 1 , и проведем прямые AB 1 и DС 1 .

Так как ребра AD и B 1 С 1 соответственно равны и параллельны ребру BС, то они равны и параллельны между собой.

Вследствие этого фигура ADС 1 B 1 есть параллелограмм, в котором С 1 A и DB 1 - диагонали, а в параллелограмме диагонали пересекаются пополам.

Это доказательство можно повторить о каждых двух диагоналях.

Поэтому диагональ AC 1 пересекается с BD 1 пополам, диагональ BD 1 с A 1 С пополам.

Таким образом, все диагонали пересекаются пополам и, следовательно, в одной точке.

Теорема. В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трех его измерений.

Пусть (рис.) AC 1 есть какая-нибудь диагональ прямоугольного параллелепипеда.

Проведя AC, получим два треугольника: AC 1 С и ACB. Оба они прямоугольные:

первый потому, что параллелепипед прямой, и следовательно, ребро СС 1 перпендикулярно к основанию,

второй потому, что параллелепипед прямоугольный, значит в основании его лежит прямоугольник.

Из этих треугольников находим:

AC 2 1 = AC 2 + СС 2 1 и AC 2 = AB 2 + BC 2

Следовательно, AC 2 1 = AB 2 + BC 2 + СС 2 1 = AB 2 + AD 2 + AA 2 1

Следствие. В прямоугольном параллелепипеде все диагонали равны .

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо - в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ - раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности - включая административные, технические и физические - для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

На этом уроке все желающие смогут изучить тему «Прямоугольный параллелепипед». В начале урока мы повторим, что такое произвольный и прямой параллелепипеды, вспомним свойства их противоположных граней и диагоналей параллелепипеда. Затем рассмотрим, что такое прямоугольный параллелепипед, и обсудим его основные свойства.

Тема: Перпендикулярность прямых и плоскостей

Урок: Прямоугольный параллелепипед

Поверхность, составленная из двух равных параллелограммов АВСD и А 1 В 1 С 1 D 1 и четырех параллелограммов АВВ 1 А 1 , ВСС 1 В 1 , СDD 1 С 1 , DАА 1 D 1 , называется параллелепипедом (рис. 1).

Рис. 1 Параллелепипед

То есть: имеем два равных параллелограмма АВСD и А 1 В 1 С 1 D 1 (основания), они лежат в параллельных плоскостях так, что боковые ребра АА 1 , ВВ 1 , DD 1 , СС 1 параллельны. Таким образом, составленная из параллелограммов поверхность называется параллелепипедом .

Таким образом, поверхность параллелепипеда - это сумма всех параллелограммов, из которых составлен параллелепипед.

1. Противоположные грани параллелепипеда параллельны и равны.

(фигуры равны, то есть их можно совместить наложением)

Например:

АВСD = А 1 В 1 С 1 D 1 (равные параллелограммы по определению),

АА 1 В 1 В = DD 1 С 1 С (так как АА 1 В 1 В и DD 1 С 1 С - противоположные грани параллелепипеда),

АА 1 D 1 D = ВВ 1 С 1 С (так как АА 1 D 1 D и ВВ 1 С 1 С - противоположные грани параллелепипеда).

2. Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.

Диагонали параллелепипеда АС 1 , В 1 D, А 1 С, D 1 В пересекаются в одной точке О, и каждая диагональ делится этой точкой пополам (рис. 2).

Рис. 2 Диагонали параллелепипеда пересекаются и деляться точкой пересечения пополам.

3. Имеются три четверки равных и параллельных ребер параллелепипеда : 1 - АВ, А 1 В 1 , D 1 C 1 , DC, 2 - AD, A 1 D 1 , B 1 C 1 , BC, 3 - АА 1 , ВВ 1 , СС 1 , DD 1 .

Определение. Параллелепипед называется прямым, если его боковые ребра перпендикулярны основаниям.

Пусть боковое ребро АА 1 перпендикулярно основанию (рис. 3). Это означает, что прямая АА 1 перпендикулярна прямым АD и АВ, которые лежат в плоскости основания. А, значит, в боковых гранях лежат прямоугольники. А в основаниях лежат произвольные параллелограммы. Обозначим, ∠BAD = φ, угол φ может быть любым.

Рис. 3 Прямой параллелепипед

Итак, прямой параллелепипед - это параллелепипед, в котором боковые ребра перпендикулярны основаниям параллелепипеда.

Определение. Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию. Основания являются прямоугольниками.

Параллелепипед АВСDА 1 В 1 С 1 D 1 - прямоугольный (рис. 4), если:

1. АА 1 ⊥ АВСD (боковое ребро перпендикулярно плоскости основания, то есть параллелепипед прямой).

2. ∠ВАD = 90°, т. е. в основании лежит прямоугольник.

Рис. 4 Прямоугольный параллелепипед

Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда. Но есть дополнительные свойства, которые выводятся из определения прямоугольного параллелепипеда.

Итак, прямоугольный параллелепипед - это параллелепипед, у которого боковые ребра перпендикулярны основанию. Основание прямоугольного параллелепипеда - прямоугольник .

1. В прямоугольном параллелепипеде все шесть граней прямоугольники.

АВСD и А 1 В 1 С 1 D 1 - прямоугольники по определению.

2. Боковые ребра перпендикулярны основанию . Значит, все боковые грани прямоугольного параллелепипеда - прямоугольники.

3. Все двугранные углы прямоугольного параллелепипеда прямые.

Рассмотрим, например, двугранный угол прямоугольного параллелепипеда с ребром АВ, т. е. двугранный угол между плоскостями АВВ 1 и АВС.

АВ - ребро, точка А 1 лежит в одной плоскости - в плоскости АВВ 1 , а точка D в другой - в плоскости А 1 В 1 С 1 D 1 . Тогда рассматриваемый двугранный угол можно еще обозначить следующим образом: ∠А 1 АВD.

Возьмем точку А на ребре АВ. АА 1 - перпендикуляр к ребру АВ в плоскости АВВ- 1 , AD перпендикуляр к ребру АВ в плоскости АВС. Значит, ∠А 1 АD - линейный угол данного двугранного угла. ∠А 1 АD = 90°, значит, двугранный угол при ребре АВ равен 90°.

∠(АВВ 1 , АВС) = ∠(АВ) = ∠А 1 АВD= ∠А 1 АD = 90°.

Аналогично доказывается, что любые двугранные углы прямоугольного параллелепипеда прямые.

Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

Примечание. Длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда, являются измерениями прямоугольного параллелепипеда. Их иногда называют длина, ширина, высота.

Дано: АВСDА 1 В 1 С 1 D 1 - прямоугольный параллелепипед (рис. 5).

Доказать: .

Рис. 5 Прямоугольный параллелепипед

Доказательство:

Прямая СС 1 перпендикулярна плоскости АВС, а значит, и прямой АС. Значит, треугольник СС 1 А - прямоугольный. По теореме Пифагора:

Рассмотрим прямоугольный треугольник АВС. По теореме Пифагора:

Но ВС и AD - противоположные стороны прямоугольника. Значит, ВС = AD. Тогда:

Так как , а , то. Поскольку СС 1 = АА 1 , то что и требовалось доказать.

Диагонали прямоугольного параллелепипеда равны.

Обозначим измерения параллелепипеда АВС как a, b, c (см. рис. 6), тогда АС 1 = СА 1 = В 1 D = DВ 1 =

Прямоугольный параллелепипед – это разновидность многогранника, состоящая из 6 граней, всякая из которых является прямоугольником. В свою очередь, диагональ – это отрезок, тот, что соединяет противоположные вершины параллелограмма. Его длину дозволено обнаружить двумя способами.

Вам понадобится

• Знание длины всех сторон параллелограмма.

Инструкция

1. Способ 1. Дан прямоугольный параллелепипед со сторонами a, b, c и диагональю d. Согласно одному из свойств параллелограмма, квадрат диагонали равен сумме квадратов 3 его сторон. Отсель следует, что сама длина диагонали может быть рассчитана с поддержкой извлечения квадрата из данной суммы (рис.1).

2. Способ 2. Возможен, что прямоугольный параллелепипед является кубом. Куб – это такой прямоугольный параллелепипед, у которого всякая грань представлена квадратом. Следственно, все его стороны равны. Тогда формула для расчеты длины его диагонали будет выражена так:d = a*?3

Параллелепипед – частный случай призмы, у которой все шесть граней являются параллелограммами либо прямоугольниками. Параллелепипед с прямоугольными гранями называют также прямоугольным. У параллелепипеда имеется четыре пересекающиеся диагонали. Если даны три ребра а, b, с, обнаружить все диагонали прямоугольного параллелепипеда дозволено, исполняя добавочные построения.

Инструкция

1. Нарисуйте прямоугольный параллелепипед. Запишите вестимые данные: три ребра а, b, с. Сначала постройте одну диагональ m. Для ее определения используем качество прямоугольного параллелепипеда, согласно которому все его углы являются прямыми.

2. Постройте диагональ n одной из граней параллелепипеда. Построение проведите так, дабы знаменитое ребро, желанная диагональ параллелепипеда и диагональ грани совместно образовывали прямоугольный треугольник а, n, m.

3. Обнаружьте построенную диагональ грани. Она является гипотенузой иного прямоугольного треугольника b, с, n. Согласно теореме Пифагора n² = с² + b². Вычислите данное выражение и возьмите корень квадратный из полученного значения – это будет диагональ грани n.

4. Обнаружьте диагональ параллелепипеда m. Для этого в прямоугольном треугольнике а, n, m обнаружьте незнакомую гипотенузу: m² = n² + a². Подставьте вестимые значения, после этого вычислите корень квадратный. Полученный итог и будет первой диагональю параллелепипеда m.

5. Аналогичным образом проведите ступенчато все остальные три диагонали параллелепипеда. Также для всей из них исполните добавочные построения диагоналей прилегающих граней. Рассматривая образуемые прямоугольные треугольники и применяя теорему Пифагора, обнаружьте значения остальных диагоналей прямоугольного параллелепипеда.

Видео по теме

Форму параллелепипеда имеют многие настоящие объекты. Примерами являются комната и бассейн. Детали, имеющие такую форму – не редкость и в промышленности. По этой причине зачастую появляется задача нахождения объема данной фигуры.

Инструкция

1. Параллелепипед представляет собой призму, основанием которой является параллелограмм. У параллелепипеда имеются грани – все плоскости, формирующие данную фигуру. Каждого у него насчитывается шесть граней, причем, все они являются параллелограммами. Его противоположные грани между собой равны и параллельны. Помимо того, он имеет диагонали, которые пересекаются в одной точке и в ней делятся напополам.

2. Параллелепипед бывает 2-х видов. У первого все грани являются параллелограммами, а у второго – прямоугольниками. Конечный из них именуется прямоугольным параллелепипедом. У него все грани прямоугольные, а боковые грани перпендикулярны к основанию. Если прямоугольный параллелепипед имеет грани, основы которых – квадраты, то он именуется кубом. В этом случае, его грани и ребра равны. Ребром именуется сторона всякого многогранника, к числу которых относится и параллелепипед.

3. Для того, дабы обнаружить объем параллелепипеда, нужно знать площадь его основания и высоту. Объем находится исходя из того, какой именно параллелепипед фигурирует в условиях задачи. У обычного параллелепипеда в основании находится параллелограмм, а у прямоугольного – прямоугольник либо квадрат, у которого неизменно углы прямые. Если в основании параллелепипеда лежит параллелограмм, то его объем находится дальнейшим образом:V=S*H, где S – площадь основания, H -высота параллелепипедаВысотой параллелепипеда обыкновенно выступает его боковое ребро. В основании параллелепипеда может лежать и параллелограмм, не являющийся прямоугольником. Из курса планиметрии знаменито, что площадь параллелограмма равна:S=a*h, где h – высота параллелограмма, a – длина основания, т.е. :V=a*hp*H

4. Если имеет место 2-й случай, когда основание параллелепипеда – прямоугольник, то объем вычисляется по той же формуле, но площадь основания находится несколько другим образом:V=S*H,S=a*b, где a и b – соответственно, стороны прямоугольника и ребра параллелепипеда.V=a*b*H

5. Для нахождения объема куба следует руководствоваться примитивными логическими методами. От того что все грани и ребра куба равны, а в основании куба – квадрат, руководствуясь формулами, указанными выше, дозволено вывести следующую формулу:V=a^3

Замкнутая геометрическая фигура, образованная двумя парами лежащих друг наоборот друга параллельных отрезков идентичной длины, именуется параллелограммом. А параллелограмм, все углы которого равны 90°, называют еще и прямоугольником. В этой фигуре дозволено провести два отрезка идентичной длины, соединяющих противоположные вершины – диагонали. Длина этих диагоналей вычисляется несколькими методами.

Инструкция

1. Если знамениты длины 2-х смежных сторон прямоугольника (А и В), то длину диагонали (С) определить дюже примитивно. Исходите из того, что диагональ лежит наоборот прямого угла в треугольнике, образуемом ею и этими двумя сторонами. Это разрешает применить в расчетах теорему Пифагора и вычислить длину диагонали, обнаружив квадратный корень из суммы возведенных в квадрат длин вестимых сторон: С=v(А?+В?).

2. Если вестима длина лишь одной стороны прямоугольника (А), а также величина угла (?), тот, что с ней образует диагональ , то для вычисления длины этой диагонали (С) придется применять одну из прямых тригонометрических функций – косинус. Поделите длину вестимой стороны на косинус знаменитого угла – это и будет желанная длина диагонали: С=А/cos(?).

3. Если прямоугольник задан координатами своих вершин, то задача вычисления длины его диагонали сведется к нахождению расстояния между двумя точками в этой системе координат. Примените теорему Пифагора к треугольнику, тот, что образуют проекции диагонали на всякую из координатных осей. Возможен, прямоугольник в двухмерных координатах образован вершинами A(X?;Y?), B(X?;Y?), C(X?;Y?) и D(X?;Y?). Тогда вам необходимо вычислить расстояние между точками A и C. Длина проекции этого отрезка на ось X будет равна модулю разности координат |X?-X?|, а проекции на ось Y – |Y?-Y?|. Угол между осями равен 90°, из чего вытекает, что эти две проекции являются катетами, а длина диагонали (гипотенузы) равна квадратному корню из суммы квадратов их длин: AC=v((X?-X?)?+(Y?-Y?)?).

4. Для нахождения диагонали прямоугольника в трехмерной системе координат действуйте так же, как в предыдущем шаге, лишь добавив в формулу длину проекции на третью координатную ось: AC=v((X?-X?)?+(Y?-Y?)?+(Z?-Z?)?).

Видео по теме

В памяти многих осталась математическая прибаутка: Пифагоровы штаны во все стороны равны. Воспользуйтесь ею, дабы вычислить диагональ прямоугольника .

Вам понадобится

• Лист бумаги, линейка, карандаш, калькулятор с функцией вычисления корней.

Инструкция

1. Прямоугольник – это четырехугольник, все углы которого прямые. Диагональ прямоугольника – отрезок прямой, соединяющий две противоположные его вершины.

2. На листе бумаги с поддержкой линейки и карандаша нарисуйте произвольный прямоугольник АВСD. Класснее это сделать на тетрадном листе в клетку – так проще будет нарисовать прямые углы. Объедините отрезком вершины прямоугольника А и С. Полученный отрезок АС является диагональ ю прямоугольника АВСD.

3. Обратите внимание, диагональ АС поделила прямоугольник АВСD на треугольники АВС и АСD. Полученные треугольники АВС и АСD – прямые треугольники, т.к. углы АВС и АDС равны 90 градусам (по определению прямоугольника ). Припомните теорему Пифагора – квадрат гипотенузы равен сумме квадратов катетов.

4. Гипотенуза – это сторона треугольника, противолежащая прямому углу. Катеты – стороны треугольника, прилежащие к прямому углу. Применительно к треугольникам АВС и АСD: АВ и ВС, АD и DC– катеты, АС – всеобщая гипотенуза для обоих треугольников (желанная диагональ ). Следственно, АС в квадрате = квадрат АВ + квадрат ВС либо АС в квадрате = квадрат АD + квадрат DС. Подставьте значения длин сторон прямоугольника в вышеприведенную формулу и вычислите длину гипотенузы (диагонали прямоугольника ).

5. Скажем, стороны прямоугольника АВСD равны дальнейшим значениям: АВ = 5 см и ВС = 7см. Квадрат диагонали АС данного прямоугольника рассчитывается по теореме Пифагора: АС в квадрате = квадрат АВ + квадрат ВС = 52+72 = 25 + 49 = 74 кв.см. С подмогой калькулятора вычислите значение квадратного корня 74. У вас должно получиться 8,6 см (округленное значение). Имейте в виду, что по одному из свойств прямоугольника , его диагонали равны. Значит длина 2-й диагонали BD прямоугольника АВСD равна длине диагонали АС. Для вышеприведенного примера эта величина составляет 8,6 см.

Видео по теме

Совет 6: Как обнаружить диагональ параллелограмма, если даны стороны

Параллелограмм – это четырехугольник, противоположные стороны которого параллельны. Прямые, соединяющие его противоположные углы, именуются диагоналями. Их длина зависит не только от длин сторон фигуры, но и от величин углов в вершинах этого многоугольника, следственно без познания правда бы одного из углов вычислить длины диагоналей дозволено только в исключительных случаях. Таковыми являются частные случаи параллелограмма – квадрат и прямоугольник.

Инструкция

1. Если длины всех сторон параллелограмма идентичны (a), то эту фигуру дозволено назвать еще и квадратом. Величины всех его углов равны 90°, а длины диагоналей (L) идентичны и могут быть рассчитаны по теореме Пифагора для прямоугольного треугольника. Умножьте длину стороны квадрата на корень из двойки – итог и будет длиной всякой из его диагоналей: L=a*?2.

2. Если о параллелограмме знаменито, что он является прямоугольником с указанными в условиях длиной (a) и шириной (b), то и в этом случае длины диагоналей (L) будут равны. И тут тоже задействуйте теорему Пифагора для треугольника, в котором гипотенузой является диагональ, а катетами – две смежные стороны четырехугольника. Желанную величину рассчитайте извлечением корня из суммы возведенных в квадрат ширины и высоты прямоугольника: L=?(a?+b?).

3. Для всех остальных случаев умения одних только длин сторон хватит лишь для определения величины, включающей в себя длины сразу обеих диагоналей – сумма их квадратов по определению равна удвоенной сумме квадратов длин сторон. Если же в дополнение к длинам 2-х смежных сторон параллелограмма (a и b) знаменит еще и угол между ними (?), то это дозволит рассчитать длины всякого отрезка, соединяющего противоположные углы фигуры. Длину диагонали (L?), лежащей наоборот вестимого угла, обнаружьте по теореме косинусов – сложите квадраты длин смежных сторон, от итога отнимите произведение этих же длин на косинус угла между ними, а из полученной величины извлеките квадратный корень: L? = ?(a?+b?-2*a*b*cos(?)). Для нахождения длины иной диагонали (L?) дозволено воспользоваться свойством параллелограмма, приведенным в начале этого шага – удвойте сумму квадратов длин 2-х сторон, от итога отнимите квадрат теснее рассчитанной диагонали, а из полученного значения извлеките корень. В всеобщем виде эту формулу дозволено записать так: L? = ?(a?+b?- L??) = ?(a?+b?-(a?+b?-2*a*b*cos(?))) = ?(a?+b?-a?-b?+2*a*b*cos(?)) = ?(2*a*b*cos(?)).