The angle between intersecting straight lines in space. Angle between crossing lines (2019)

To use presentation previews, create a Google account and log in to it: https://accounts.google.com

Slide captions:

Angle between straight lines

Goals and objectives of the lesson: To form the concept of an angle between: Intersecting; Parallel; crossing straight lines. Learn to find the angle between: Intersecting; parallel; crossing straight lines.

Let's remember: The base of the prism ABCDA 1 B 1 C 1 D 1 is a trapezoid. Which of the following pairs of lines are crossing lines?

The location of lines in space and the angle between them 1. Intersecting lines. 2. Parallel lines. 3. Crossing lines.

Any two intersecting lines lie in the same plane and form four undeveloped angles.

If intersecting lines form four equal angles, then the angle between these lines is 90°. a b

The angle between two parallel lines is 0°.

The angle between two intersecting lines in space is the smallest of the angles formed by the rays of these lines with the vertex at the point of their intersection.

The angle between intersecting lines a and b is the angle between the constructed intersecting lines and.

The angle between intersecting straight lines, as well as between straight lines of the same plane, cannot be more than 90°. Two intersecting lines that form an angle of 90° are called perpendicular. a b a 1 c c 1 d

Angle between skew lines Let AB and CD be two skew lines. Let's take an arbitrary point M 1 in space and draw through it lines A 1 B 1 and C 1 D 1, respectively, parallel to lines AB and CD. A B C D A 1 B 1 C 1 D 1 M 1 φ If the angle between lines A 1 B 1 and C 1 D 1 is equal to φ, then we will say that the angle between the crossing lines AB and CD is equal to φ.

Let's find the angle between the skew lines AB and CD. As a point M 1, you can take any point on one of the skew lines. A B C D M 1 A 1 B 1 φ

Exercise for the eyes

Show perpendicular intersecting lines in the environment.

An image of a cube is given. Find the angle between intersecting lines a and b. 90° 45° Answer Answer

An image of a cube is given. Find the angle between intersecting lines a and b. 90° 60° Answer Answer

An image of a cube is given. Find the angle between intersecting lines a and b 90° 90° Answer Answer

Homework: §4 (pp. 85-89), No. 268, No. 269.

Physical education minute

Problem No. 1 In a regular pyramid SABCD, all edges of which are equal to 1, point E is the middle of edge SC. Find the angle between lines AD and BE.

Work in class: Tasks: No. 263 No. 265 No. 267

Preview:

I APPROVED

Math teacher

L. R. Volnyak

"__" ________ 2016

Subject : "Angle between straight lines"

Educational:

Educational:

Educational:

Lesson type: Learning new material.

Methods: verbal (story), visual (presentation), dialogical.

1. Organizational moment.

• Greetings.

1. Updating knowledge.

1. What is the relative position of two lines in space?
2. How many angles are formed when two straight lines intersect in space?
3. How to determine the angle between intersecting lines?

Slad3

1. ABCDA prism base 1 B 1 C 1 D 1 – trapezoid. Which of the following pairs of lines are crossing lines?

Answer: AB and CC 1, A 1 D 1 and CC 1.

1. Learning new material.

Slide 4

The location of lines in space and the angle between them.

1. Intersecting lines.
2. Parallel lines.
3. Crossing straight lines.

Slide 5

Any two intersecting lines lie in the same plane and form four undeveloped angles.

Slide 6

If intersecting lines form four equal angles, then the angle between these lines is 90°.

Slide 7

The angle between two parallel lines is 0°.

Slide 8

The angle between two intersecting lines in space is the smallest of the angles formed by the rays of these lines with the vertex at the point of their intersection.

Slide 9 a and b and .

Slide 10

The angle between intersecting straight lines, as well as between straight lines of the same plane, cannot be more than 90°. Two intersecting lines that form an angle of 90° are called perpendicular.

Slide 11

The angle between crossing lines.

Let AB and CD be two skew lines.

Let's take an arbitrary point M 1 space and draw lines A through it 1 B 1 and C 1 D 1 , respectively, parallel to straight lines AB and CD.

If the angle between lines A 1 B 1 and C 1 D 1 is equal to φ, then we will say that the angle between the crossing lines AB and CD is equal to φ.

Slide 12

Let's find the angle between the crossing lines AB and CD.

As point M 1 you can take any point on one of the crossing lines.

Slide 13

Physical education minute

Slide 14

1. Show perpendicular intersecting lines in the environment.

Slide 15

2. An image of a cube is given. Find the angle between intersecting lines a and b.

a) 90°; b) 45°;

Slide 16

c) 60°; d) 90°;

Slide 17

e) 90°; e) 90°.

1. Consolidating new material

Slide 19

Physical education minute

Slide 20

№1.

In the right pyramid SABCD , all edges of which are equal to 1, point E – middle of the rib S.C. .Find the angle between the lines AD and BE.

Solution:

Required angle = angle C.B.E. .Triangle SBC-equilateral.

BE – angle bisector = 60. Angle CBE is 30.

Answer: 30°.

№263.

Answer:

Angle between intersecting lines a and b called the angle between the constructed intersecting lines a 1 and b 1, with a 1 || a, b 1 || b.

№265.

The angle between straight lines a and b is equal to 90°. Is it true that lines a and b intersect?

Answer:

Incorrect because lines can either intersect or intersect.

№267.

DABC is a tetrahedron, points O and F are the midpoints of edges AD and CD, respectively, segment TK is the midline of triangle ABC.

1. What is the angle between lines OF and CB?
2. Is it true that the angle between lines OF and TK is equal to 60°?
3. What is the angle between lines TF and DB?

Solution:

Given: DABC,

O – middle AD,

F – middle CD,

TC – middle line ∆ABC.

Solution:

1. Reflection

• What new have we learned?
• Have we completed the tasks that were assigned at the beginning of the lesson?
• What problems have we learned to solve?

1. Homework.

§4 (pp. 85-89), No. 268, No. 269.

Preview:

I APPROVED

Math teacher

L. R. Volnyak

"__" ________ 2016

Subject : "Angle between straight lines"

Educational: with the help of practical tasks, ensure that students understand the definition of the angle between intersecting, parallel and intersecting lines;

Educational: develop students’ spatial imagination when solving geometric problems, geometric thinking, interest in the subject, cognitive and creative activity students, mathematical speech, memory, attention; develop independence in mastering new knowledge.

Educational: to instill in students a responsible attitude towards educational work, strong-willed qualities; form emotional culture and communication culture.

Lesson type: generalization and systematization of knowledge and skills.

Methods: verbal (story), dialogical.

1. Organizational moment.

• Greetings.
• Communicating the goals and objectives of the lesson.
• Motivation for learning new material.
• Psychological and pedagogical attunement of students for upcoming activities.
• Checking those present in the lesson;

1. Checking homework

№268

ABCDA 1 B 1 C 1 D 1 – cuboid, point O and T are the midpoints of the edges SS 1 and DD 1 respectively. a) Is it true that the angle between lines AD and TO is 90°? b) What is the angle between the lines A? 1 B 1 and BC?

Solution:

a) True, since TO || DC =>(AD, TO) = ADC = 90° (ABCD – rectangle).

b)BC || B 1 C 1 => (A 1 B 1, BC) = A 1 B 1 C 1 = 90°.

Answer: 90°, 90°.

№269

ABCDA 1 B 1 C 1 D 1 – cube a) Is it true that the angle between the lines A 1 B and C 1 D equals 90°? b) Find the angle between lines B 1 O and C 1 D. c) Is it true that the angle between straight lines AC and C 1 D equals 45°?

Solution:

a) True, because B 1 A || C 1 D => (A 1 B, C 1 D)= (B 1 A, A 1 B) = 90°, as the angle between the diagonals of a square.

b) 1. V 1 A || C 1 D=> (B 1 O, C 1 D) = AB 1 O.

2. in Δ AB 1 C AB 1 = B 1 C = AC as diagonals of equal squares B 1 O – median and bisector AB 1 С=60° => AB 1 O=30°.

c) no, since C 1 D || BA => (AC, C 1 D)= B 1 AC=60° as equilateral angle Δ AB 1 S.

Answer: b) 30°.

1. Updating knowledge.

Method: frontal interview (orally):

1. What sections does geometry study?
2. What is the angle between parallel lines?
3. What shapes does planimetry study and what shapes does stereometry study?
4. Which angle is called a crossing angle?
5. What are two straight lines that intersect and form an angle of 90° called?

1. Consolidation of what has been learned.

Dictation (10 min):

Option 1:

The edge of the cube is equal to A .

Find: (AB 1,CC 1)

Solution:

СС1‖ВВ1

(AB1,CC1)= AB1B

АВ1В=45˚

Answer: (AB1,CC1)=45˚

1. Let a and b be skew lines, and let b 1 || b. Is it true that the angle between lines a and b is equal to the angle between lines a and b 1 ? If so, why?

Option 2:

1. What angle is called the angle between intersecting lines?

The edge of the cube is equal to A .

AB And WITHD crossed by the third straight line MN, then the angles formed in this case receive the following names in pairs:

corresponding angles: 1 and 5, 4 and 8, 2 and 6, 3 and 7;

internal crosswise angles: 3 and 5, 4 and 6;

external crosswise angles: 1 and 7, 2 and 8;

internal one-sided corners: 3 and 6, 4 and 5;

external one-sided corners: 1 and 8, 2 and 7.

So, ∠ 2 = ∠ 4 and ∠ 8 = ∠ 6, but according to what has been proven, ∠ 4 = ∠ 6.

Therefore, ∠ 2 =∠ 8.

3. Corresponding angles 2 and 6 are the same, since ∠ 2 = ∠ 4, and ∠ 4 = ∠ 6. Let’s also make sure that the other corresponding angles are equal.

4. Sum internal one-sided corners 3 and 6 will be 2d because the sum adjacent corners 3 and 4 is equal to 2d = 180 0, and ∠ 4 can be replaced by the identical ∠ 6. We also make sure that sum of angles 4 and 5 is equal to 2d.

5. Sum external one-sided corners will be 2d because these angles are equal respectively internal one-sided corners like corners vertical.

From the above proven justification we obtain converse theorems.

When, at the intersection of two lines with an arbitrary third line, we obtain that:

1. Internal crosswise angles are the same;

or 2. External crosswise angles are identical;

or 3. Corresponding angles are equal;

or 4. The sum of internal one-sided angles is 2d = 180 0;

or 5. The sum of external one-sided ones is 2d = 180 0 ,

then the first two lines are parallel.

In this lesson we will give the definition of codirectional rays and prove the theorem on the equality of angles with codirectional sides. Next, we will give the definition of the angle between intersecting lines and skew lines. Let's consider what the angle between two straight lines can be. At the end of the lesson, we will solve several problems on finding angles between intersecting lines.

Topic: Parallelism of lines and planes

Lesson: Angles with aligned sides. Angle between two straight lines

Any straight line, for example OO 1(Fig. 1.), cuts the plane into two half-planes. If the rays OA And O 1 A 1 are parallel and lie in the same half-plane, then they are called co-directed.

Rays O 2 A 2 And OA are not co-directional (Fig. 1.). They are parallel, but do not lie in the same half-plane.

If the sides of two angles are aligned, then the angles are equal.

Proof

Let us be given parallel rays OA And O 1 A 1 and parallel rays OB And About 1 In 1(Fig. 2.). That is, we have two angles AOB And A 1 O 1 B 1, whose sides lie on codirectional rays. Let us prove that these angles are equal.

On the beam side OA And O 1 A 1 select points A And A 1 so that the segments OA And O 1 A 1 were equal. Likewise, points IN And B 1 choose so that the segments OB And About 1 In 1 were equal.

Consider a quadrilateral A 1 O 1 OA(Fig. 3.) OA And O 1 A 1 A 1 O 1 OA A 1 O 1 OA OO 1 And AA 1 parallel and equal.

Consider a quadrilateral B 1 O 1 OV. This quadrilateral side OB And About 1 In 1 parallel and equal. Based on parallelogram, quadrilateral B 1 O 1 OV is a parallelogram. Because B 1 O 1 OV- parallelogram, then the sides OO 1 And BB 1 parallel and equal.

And straight AA 1 parallel to the line OO 1, and straight BB 1 parallel to the line OO 1, means straight AA 1 And BB 1 parallel.

Consider a quadrilateral B 1 A 1 AB. This quadrilateral side AA 1 And BB 1 parallel and equal. Based on parallelogram, quadrilateral B 1 A 1 AB is a parallelogram. Because B 1 A 1 AB- parallelogram, then the sides AB And A 1 B 1 parallel and equal.

Consider triangles AOB And A 1 O 1 B 1. Parties OA And O 1 A 1 equal in construction. Parties OB And About 1 In 1 are also equal in construction. And as we have proven, both sides AB And A 1 B 1 are also equal. So triangles AOB And A 1 O 1 B 1 equal on three sides. In equal triangles, equal angles lie opposite equal sides. So the angles AOB And A 1 O 1 B 1 are equal, as required to prove.

1) Intersecting lines.

If the lines intersect, then we have four different angles. Angle between two straight lines, is called the smallest angle between two straight lines. Angle between intersecting lines A And b let us denote α (Fig. 4.). The angle α is such that .

Rice. 4. Angle between two intersecting lines

2) Crossing lines

Let straight A And b interbreeding. Let's choose an arbitrary point ABOUT. Through the point ABOUT let's make a direct a 1, parallel to the line A, and straight b 1, parallel to the line b(Fig. 5.). Direct a 1 And b 1 intersect at a point ABOUT. Angle between two intersecting lines a 1 And b 1, angle φ, and is called the angle between intersecting lines.

Rice. 5. Angle between two intersecting lines

Does the size of the angle depend on the selected point O? Let's choose a point O 1. Through the point O 1 let's make a direct a 2, parallel to the line A, and straight b 2, parallel to the line b(Fig. 6.). Angle between intersecting lines a 2 And b 2 let's denote φ 1. Then the angles φ And φ 1 - corners with aligned sides. As we have proven, such angles are equal to each other. This means that the magnitude of the angle between intersecting lines does not depend on the choice of point ABOUT.

Direct OB And CD parallel, OA And CD interbreed. Find the angle between the lines OA And CD, If:

1) ∠AOB= 40°.

Let's choose a point WITH. Pass a straight line through it CD. Let's carry out CA 1 parallel OA(Fig. 7.). Then the angle A 1 CD- angle between intersecting lines OA And CD. According to the theorem about angles with concurrent sides, the angle A 1 CD equal to angle AOB, that is 40°.

Rice. 7. Find the angle between two straight lines

2) ∠AOB= 135°.

Let's do the same construction (Fig. 8.). Then the angle between the crossing lines OA And CD is equal to 45°, since it is the smallest of the angles that are obtained when straight lines intersect CD And CA 1.

3) ∠AOB= 90°.

Let's do the same construction (Fig. 9.). Then all the angles that are obtained when the lines intersect CD And CA 1 equal 90°. The required angle is 90°.

1) Prove that the midpoints of the sides of a spatial quadrilateral are the vertices of a parallelogram.

Proof

Let us be given a spatial quadrilateral ABCD. M,N,K,L- middle of ribs B.D.A.D.AC,B.C. accordingly (Fig. 10.). It is necessary to prove that MNKL- parallelogram.

Consider a triangle ABD. MN MN parallel AB and equals half of it.

Consider a triangle ABC. LK- middle line. According to the property of the midline, LK parallel AB and equals half of it.

AND MN, And LK parallel AB. Means, MN parallel LK by the theorem of three parallel lines.

We find that in a quadrilateral MNKL- sides MN And LK parallel and equal, since MN And LK equal to half AB. So, according to the parallelogram criterion, a quadrilateral MNKL- a parallelogram, which is what needed to be proven.

2) Find the angle between the lines AB And CD, if the angle MNK= 135°.

As we have already proven, MN parallel to the line AB. NK- middle line of the triangle ACD, by property, NK parallel DC. So, through the point N there are two straight lines MN And NK, which are parallel to skew lines AB And DC respectively. So, the angle between the lines MN And NK is the angle between intersecting lines AB And DC. We are given an obtuse angle MNK= 135°. Angle between straight lines MN And NK- the smallest of the angles obtained by intersecting these lines, that is, 45°.

So, we looked at angles with codirectional sides and proved their equality. We looked at the angles between intersecting and skewing lines and solved several problems on finding the angle between two lines. In the next lesson we will continue solving problems and reviewing theory.

1. Geometry. Grades 10-11: textbook for students of general education institutions (basic and specialized levels) / I. M. Smirnova, V. A. Smirnov. - 5th edition, corrected and expanded - M.: Mnemosyne, 2008. - 288 p. : ill.

2. Geometry. 10-11 grade: Textbook for general education educational institutions/ Sharygin I.F. - M.: Bustard, 1999. - 208 p.: ill.

3. Geometry. Grade 10: Textbook for general education institutions with in-depth and specialized study of mathematics /E. V. Potoskuev, L. I. Zvalich. - 6th edition, stereotype. - M.: Bustard, 008. - 233 p. :il.

IN) B.C. And D 1 B 1.

Rice. 11. Find the angle between lines

4. Geometry. Grades 10-11: textbook for students of general education institutions (basic and specialized levels) / I. M. Smirnova, V. A. Smirnov. - 5th edition, corrected and expanded - M.: Mnemosyne, 2008. - 288 pp.: ill.

Tasks 13, 14, 15 p. 54

Entrepreneurship as a self-organizing system exists and develops under the influence of a system of factors. At the end of the 70s. XX century Researchers such as T. Bachkai, D. Mesena, D. Miko and others, studying the effect of risk factors, indicated that they are all interconnected. Along with "natural"...

ASSESSMENT OF THE AMOUNT OF RISK AND CRITERIA FOR SELECTION OF A SOLUTION

Risk management is impossible without assessing its magnitude. The assessment method depends on the type of risk. Taking into account the variety of risks and the complexity of their management tasks, three types of assessments are used in practice: qualitative, axiological and quantitative. Qualitative risk assessment is widely used and allows...
(Risks in accounting)

Intersecting lines

If straight lines intersect, then their projections of the same name intersect each other at a point that is the projection of the point of intersection of these lines. Indeed (Figure 2.30), if the point TO belongs to both lines AB And CD, then the projection of this point must be the intersection point...
(Engineering graphics)

Crossing lines

Crossing straight lines do not intersect or parallel each other. Figure 2.32 shows two crossing lines general position: although projections of the same name intersect each other, their points of intersection cannot be connected by a connection line parallel to the connection lines L"L" And...
(Engineering graphics)

DISTANCE BETWEEN CROSSING STRAIGHTS

Distance between crossing lines A And Kommersant determined by the length of the perpendicular segment KM, intersecting both lines (and _1_ KM; Y.KM) (Fig. 349, b, c). The problem is solved simply if one of the lines is projecting. Let, for example, a±Pn then the required segment KM...
(Descriptive geometry)

The relative position of a straight line and a plane, two planes

Signs of the relative position of a straight line and a plane, two planes Let us recall the signs of the relative position of a line and a plane, as well as two planes, familiar from stereometry. 1. If a line and a plane have one common point, then the line and the plane intersect (Fig. 3.6a). 2. If a straight line and a plane...
(Fundamentals of Engineering Graphics)

Signs of the relative position of a straight line and a plane, two planes

Let us recall the signs of the relative position of a line and a plane, as well as two planes, familiar from stereometry. 1. If a line and a plane have one common point, then the line and the plane intersect (Fig. 3.6a). 2. If a line and a plane have two common points, then the line lies in the plane (Fig. 3.66)....
(Fundamentals of Engineering Graphics)

Parallel lines. Distance between parallel lines.
.

Corresponding angles .
Internal and external crosswise angles .

Internal and external one-sided corners .

Angles with correspondingly perpendicular sides .
Proportional segments . Thales's theorem.

Two straight lines AB and CD (Fig. 11) are called parallel, if they lie in the same plane and do not intersect, no matter how long they continue. Designation: AB || CD . All points of one parallel line are at the same distance from another parallel line. All lines parallel to one line are parallel to each other. It is generally accepted that the angle between parallel lines is zero. Angle between two parallel rays is equal to zero if they have the same directions, and 180° , if their directions are opposite. All perpendiculars ( AB, CD, EF , Fig. 12) to the same straight line K.M. parallelamong themselves. Reverse, direct K.M. , perpendicular to one of parallel lines, is perpendicular to the others. Length perpendicular segment between two parallel lines, There is distance between them.

When two parallel lines intersect with a third straight line, eight angles are formed (Fig. 13), which are called in pairs:

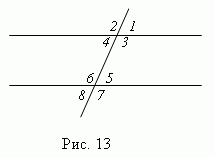
1) corresponding angles (1 And 5; 2 And 6; 3 And 7; 4 And 8 ); these angles are in pairs

are equal: ( 1 = 5; 2 = 6; 3 = 7; 4 = 8 );

2) internal crosswise angles (4 And 5; 3 And 6 ); they are pairwise equal;

3) external crosswise angles (1 And 8; 2 And 7 ); they are pairwise equal;

4) internal one-sided corners (3 And 5; 4 And 6 ); their sum is 180°

( 3 + 5 = 180 ° ; 4 + 6 = 180 ° );

5) external one-sided corners (1 And 7; 2 And 8 ); their sum is 180°

( 1 + 7 = 180° ; 2 + 8 = 180 ° ).

Angles with correspondingly parallel sides or equal to each other ( if they are both sharp or both dull, 1 = 2 , Fig. 14), or their sum is 180° ( 3 + 4 = 180°, Fig. 15).